关于肿瘤药物上市前开发的经典模式，常规是依序经历三期临床试验：I期试验中，评估新治疗方式的毒性反应，包括了解剂量限制性毒性（Dose-Limiting Toxicities， DLT）和探索最大耐受剂量（Maximum Tolerated Dose，MTD），并确定后续II试验将采纳的推荐剂量（Recommended Phase 2 Dose，RP2D）；接着进行II期试验，对新治疗方式的疗效进行初步探索；最后进行大样本III期对照试验（Adequate and well-controlled studies），对II期试验中观察到的初步疗效进行确认。可以看出，II期试验承前启后，起着关键性作用，为决定是否开展III期试验提供着最直接的疗效证据。

II期试验后是否推进开展III期试验，这个时候一个不正确的决定会带来深远的不利影响：停止开发一种有前景的治疗会使病人未来失去一种有价值的治疗选择；相反，继续开发一种无效的治疗方案却会导致各方面资源和时间的大量浪费。另外，申办方基于II期试验的发现能快速有效进行决策，对产品的抢时间尽早上市也极为重要。因此，如何科学设计出高效的II期试验受到了同行广泛的关注。

本文试从历史上经典的肿瘤II期试验设计入手，包括现代的II期试验设计，将对各种试验设计的特点进行剖析，借用例子采用常用软件SAS^®进行研究设计及其样本量实现。

一、Gehan单组两阶段设计

早在20世纪50-60年代，有效抗肿瘤药物极为少见，人们常常认为II期试验就是有效淘汰无活性药物的一个研究过程。在这样的背景下，著名统计学家Gehan等（1961）创造性提出了一种单组两阶段的试验设计。人们当时的观点是，采用新的抗肿瘤药物治疗后若患者的客观缓解率低于20%则认为它没有前途，不值得进入III期进一步试验。因此，在第一阶段会治疗并观察14例患者，若没有任何患者出现缓解，则有95%信心认为该新药的缓解率低于20%，可以拒绝它；若有1例或多例患者出现缓解，则可进入第二阶段，招募更多患者进行治疗并观察，这样才能准确估计患者用药后的缓解率情况。

在上述考虑要点外，若假设治疗后缓解率和错误拒绝率（ß）出现其它不同要求，则第一阶段样本量会有所变化。第一阶段样本量计算结果见下表（调用SAS程序%Gehan_Ph2）：

鉴于对治疗后缓解率的精度（标准误）的不同要求以及第一阶段治疗完成后缓解患者例数不同，可进一步计算第二阶段所需患者的例数。第二阶段样本量计算结果见下表（调用SAS程序%Gehan_Ph2）：

*：上表中考虑缓解率精度所用75%可信区间采用Agresti-Coull校正法（1998）进行计算。

很遗憾，Gehan的设计，尤其第二阶段样本量的估算只是出于对肿瘤客观缓解率精度要求的考虑，没有与临床实践进行很好对接，未能下缓解率有无前途的统计结论，也未很好考虑下错误结论的概率。因此，上世纪70年代随着新抗肿瘤药物开发越来越多，通过II期试验能说明药物具有潜在临床受益证据的研究设计就越发迫切，统计师做过很多尝试，其中比较经典的包括Fleming的单组两阶段设计（1982）和Simon的单组两阶段设计（1989）。

二、Fleming单组两阶段设计

著名统计学家Fleming在1982年发表文章，提出了一个两阶段设计，其前瞻性地确定了新治疗方法有前途缓解率的最低值（称为p1），满足时研究者很可能希望进一步测试该药物或治疗药物组合，同样，也确定了研究治疗无前途的缓解率最大值（p0），这种情况下研究者很可能建议不再进行进一步的试验。另外，该设计允许对两类错误即“I型错误”和“II型错误”进行限制。

该设计要求两个阶段的总样本量（n=n1+n2）足够大，以便当研究者指定该制剂值得进一步研究所需的患者总缓解最少例数（r）时，假阳性和假阴性错误率都能满足I型和II型错误的约定界限。最后，该设计规定在招募到大约一半病人（n1）后，如果出现显著的阳性或阴性结果，则可以提前停止试验。这些要求对r1和s1的界值进行指定，若第一阶段n1患者中缓解患者例数至少为r1或至多为s1时则试验将提前终止，并分别宣布试验为阳性或阴性结果。

Fleming单组两阶段设计示意图如下：

不难想象，Fleming单组两阶段设计的样本量计算，与药物被认为有前途的缓解率最低值（p1）、药物被认为无前途的缓解率最大值（p0）以及统计上允许的I型和II型错误率直接相关。不同情况下Fleming单组两阶段设计样本量计算如下表（调用SAS程序%Fleming_Ph2）：

备注1：由于Fleming的两阶段设计为固定样本量计算参数的设计，目前不是很实用，此处表格展示的是A. P. Mander等（2010）的根据Fleming思想改进的考虑因优效停止试验的Simon两阶段设计。

备注2：上表中设α和ß分别为0.05和0.10。PET0指第一阶段结束时药物被认为看不到前途提前终止试验的概率大小，PET1指第一阶段结束时药物被认为看得到前途提前终止试验的概率大小。s1指第一阶段n1例受试者中药物被认为疗效优秀可提前停止最小例数，若缓解例数>s1则认为疗效优秀达到预期可提前中止；r1指第一阶段n1例受试者中药物被认为看不到前途时缓解的最大例数，若缓解例数≤r1则认为药物疗效没达到最低要求不值得继续试验，不进入第二阶段；若缓解例数＞r1且≤s1则试验进入第二阶段。r指整个研究n例受试者中药物被认为看不到前途时缓解的最大例数，若缓解例数>r则整个研究下结论药物被认为值得进一步开发。

三、Simon单组两阶段设计

但是，Fleming两阶段设计仍有些不足，1989年著名统计学家Simon发表文章，对Fleming两阶段设计进行了优化：（1）他建议不允许因小样本的第一阶段中患者疗效突出而提前终止试验，相反，为了更加准确地估计用药后缓解率，需要继续招募第二阶段患者进行治疗并观察；（2）鉴于大多数II期试验结果都是阴性的，因此他建议在无效假设成立基础上（缓解率等于p0）选择一种平均样本量（Average Sample Number，ASN）最小的设计是合适的，即Simon Optimal设计。另外，随着样本量的增加，I型和II型错误率都将控制在预设的范围内，其中两阶段样本量之和（n1+n2=n）即总样本量最小的情况，称之为Simon Minimax设计。假设试验中第一阶段n1名受试者中观察到的缓解人数为x，则：

Ÿ 若x≤r1，下结论药物无效，试验提前结束，不进入研究第二阶段；

Ÿ 若x˃r1，则研究在备择假设Ha: p≥p1下把握度设为（1-ß），第二阶段再追加n2例受试者进行治疗并评价，若总样本量n（n=n1+n2）例受试者中出现缓解例数为r或更少，则终止试验下结论药物无效。

Simon单组两阶段设计示意图如下:

不难想象，Simon单组两阶段设计的样本量计算，与药物被认为有前途的缓解率最低值（p1）、药物被认为无前途的缓解率最大值（p0）以及统计上允许的I型和II型错误率直接相关。不同情况下Simon单组两阶段设计样本量计算如下表（调用SAS程序%Simon_Ph2）：

备注：上表中设α和ß分别为0.05和0.10。PET指第一阶段结束时药物被认为看不到前途提前终止试验的概率大小。r1指第一阶段n1例受试者中药物被认为看不到前途时缓解的最大例数，若缓解例数>r1则进入第二阶段；r指整个研究n例受试者中药物被认为看不到前途时缓解的最大例数，若缓解例数>r则整个研究下结论药物被认为值得进一步开发。ASN指平均样本量。

从实践上看，在可选治疗方式目前缺乏或较少的瘤种领域，p1通常采用被认为有前途缓解率的下限20%；当已有一些有效治疗方式时，则p1会设为30-40%甚至更高；若研究的是联合治疗，则p1通常会设为比其中最有效单药缓解率还要高10-20%。为了满足II期试验样本量规模较小，P0经常设为比P1低20%的水平，例外的情况有p0和p1分别设为5%和20%。然而，在设计研究时尤其是新治疗方式的早期研究阶段，研究团队经常会面对治疗缓解率缺乏数据和幅度波动的不确定性，无法获取一个可靠的p1。在这种情况下，统计学家Y. Lin和W.J. Shih（2004）提出了一种动态的单组两阶段设计，实现了让p1保持一定的灵活变动范围。

四、Y. Lin和W.J. Shih单组两阶段动态设计

该动态设计利用研究第一阶段结束时获得的信息，在对真实缓解率高期望（p2）和低期望（p1）分两种情况（p0<p1≤p2），重新评估最初对缓解率的假设。这样第二阶段样本量可随之作相应不同选择，同时仍控制住I型和II型错误率。假设第一阶段n1名受试者中观察到的缓解人数为x，则：

Ÿ 若x≤s1，下结论药物无效，试验提前结束，不进入研究第二阶段；

Ÿ 若s1< x≤r1，则研究在备择假设H_a: p≥p1下把握度设为（1-ß1），第二阶段再追加m2例受试者进行评价，若总样本量m（m=n1+m2）例受试者中出现缓解的例数为s或更少，则终止试验下结论药物无效；

Ÿ 若x˃r1，则研究在备择假设Ha: p≥p2下把握度设为（1-ß2），第二阶段再追加n2例受试者进行评价，若总样本量n（n=n1+n2）例受试者中出现缓解的例数为r或更少，则终止试验下结论药物无效。

Y. Lin和W.J. Shih的单组两阶段动态设计示意图如下：

不同情况下单组两阶段动态设计样本量计算如下表（调用SAS程序%Simon_adaptive_Ph2）：

备注：上表中设α，ß1和ß2分别为0.05，0.20和0.10，通常ß1≥ß2。EN0、EN1和EN2分别指在P0、P1和P2三种情况下的期望样本量；最优类型有四种，类型1指EN0最小对应的情况；类型2指EN0、EN1和EN2三者最大值最小对应的情况；类型3指总样本量N和M两者最大值最小时、EN0也最小对应的情况；类型4指总样本量N和M两者最大值最小时，EN0、EN1和EN2三者最大值也最小对应的情况。各参数对应含义如下:

s1:第一阶段失败临界值（缓解受试者小于等于此例数即不进入第二阶段）

r1:第一阶段优效临界值（缓解受试者大于此例数即认为药物优效进入优效第二阶段）

n1:第一阶段所需入组受试者例数

s: 非优效两阶段失败临界值（缓解受试者小于等于此例数即认为试验失败）

m: 非优效两阶段所需总受试者例数

r: 优效两阶段失败临界值（缓解受试者小于等于此例数即认为试验失败）

n: 优效两阶段所需总受试者例数

另一方面，针对Simon的两种设计类型，满足相同预设参数的设计往往会有很多种不同情况，取各自期望样本量和总样本量的最小值往往只有一种情况，但这两种最小值有时仍会有较大的差异。因此，在计划II期试验时，我们通常会陷入两难的境地，我们必须通过比较预期样本量和总样本量两者的最小值来最终确定一种设计。有学者认为，新治疗疗效有限时优先选择Simon Optimal设计；看好疗效时会选取Simon Minimax设计。如果受试者很难招募或者研究药物比较昂贵，Fleming设计会优于Simon设计。实际上，Jung等统计学家（2001，2004）基于贝叶斯决策理论准则，逐步在期望样本量和总样本量之间找取平衡点，提出了一种可变通的动态设计方法。

五、Jung可变通动态设计

2001年，Jung等统计学家借助绘图方法，在期望样本量和总样本量之间折中提出了一种折中设计，思路如下：通常我们在研究计划阶段，会大约设定一个本研究招募受试者的最大理想样本量N_user，其次采用Simon Minimax设计算出总样本量的最小值N_minimax，接着对总样本量在前两者之间的所有设计情况计算对应的期望样本量，最后绘制总样本量（x轴）和期望样本量（y轴）的折线图，示例如下（调用SAS程序%Simon_admissible_Ph2）：

其中假设 (p0, p1,α,β)=(0.4,0.6,0.05,0.1)，不难看出Minimax设计为 ([r1/n1,r/n] = [12/29, 27/54])，Optimal设计为([r1/n1, r/n]=[8/20, 30/61]).

该作图法思路非常简洁明了。2004年Jung等统计学家针对两阶段单组设计家族，基于伦理上解释的损耗函数按照贝叶斯决策理论准则，进一步拓展提出了变通设计，上述的Simon设计和折中设计是变通设计的特例。伦理上认为，一种设计若在无效假设成立时，其总样本量和期望样本量同时达到最小，则是最理想的。鉴于此，作者构建出不同设计下d的损耗函数如下：

其中，n(d)表示设计d对应参数下的总样本量，EN(d)表示设计d对应参数下的期望样本量，q表示概率分布，或者可以看成为各种设计下总样本量对应的权重，q∈[0, 1]。可以看出q=1实际就是Simon Minimax设计，q=0则为Simon Optimal设计。在该两种设计之间，有时我们可以找到多种变通设计，如下图2所示（调用SAS程序%Simon_admissible_Ph2）：

其中假设 (p0, p1,α,β)=(0.05,0.25,0.05,0.1)

该变通设计也可以进一步拓展适用于Fleming设计（如下图3，调用SAS程序%Fleming_admissible_Ph2），

Minimax、Optimal和可变通设计三者之间的比较

我们可以基于Fleming和Simon的思路，即有无在第一阶段因突出疗效而终止的规则，举例来比较该三种这设计，如下表：

表格内各个参数的含义参考前面类似表格。

以上表为例：对于初始参数为(p0, p1,α,β)=(0.05,0.2,0.1,0.1)的Simon 两阶段设计，若预设权重q满足q∈[0,0.091]，即更倾向于选择平均样本量最小，则此时Optimal设计([r1/n1,r/n]=[0/12,3/37])是最理想的试验设计选择；若q满足q∈(0.091,0.333]与q∈(0.333,0.630]，则是介于Optimal和Minimax之间的两种可行性设计([r1/n1,r/n]=[0/13,3/35]，[r1/n1,r/n]=[0/15,3/33])；若预设权重q满足q∈(0.630,1]，即更倾向于选择最大样本量最小（例如疾病本身较为罕见受试者较难招募），则Minimax设计([r1/n1,r/n]=[0/18,3/32])是此时最理想的试验设计选择。对于初始参数为(p0, p1,α,β)=(0.05, 0.2, 0.1, 0.1)的Fleming 两阶段设计，与上述Simon两阶段叙述同理：当q∈[0, 0.091]时选择Optimal设计；q∈(0.444, 1]时选择Minimax设计；q∈(0.091, 0.268]与q∈(0.268, 0.444]存在两种可行性设计。

六、同时考虑缓解和毒性的备用设计

随着抗肿瘤药物的开发，可备用的药物亦越来越多，疗效外药物的毒性问题也日趋得到重视。Conaway和Petroni（1995）、Bryant和Day（1995）提出了考虑治疗疗效和毒性的双变量终点的两个序贯设计，但这两个设计并未考虑到治疗效果与毒性之间的权衡，而将疗效和毒性赋予了相同的权重。在上述设计的基础上，Jin Hua（2007）提出了可以分别对疗效和毒性的边际I类错误进行控制的试验设计，以便根据实际需要对客观缓解率和毒性事件发生率的I类错误和指定不同的取值。

以两阶段设计为例，假设第一阶段n1名受试者中观察到的缓解人数r1，发生毒性事件的人数为t1，则：

Ÿ 若r1<cr1，下结论药物无效，试验提前结束，不进入研究第二阶段；

Ÿ 若t1>ct1，下结论药物毒性过强，试验提前结束，不进入研究第二阶段；

Ÿ 若r1≥cr1并且t1≤ct1，则在第二阶段追加受试者使得总样本量达到n2。若总样本量n2例受试者中出现缓解的例数为r2且r2<cr2，则终止试验下结论药物无效；若总样本量n2例受试者中出现毒性事件的例数为t2且t2>ct2，则终止试验，药物毒性过大。若总样本量n2例受试者中出现缓解的例数r2和出现毒性事件的例数t2满足r2≥cr2 且t2≤ct2，则认为药物有进一步开发的价值。

Jin的单组双终点两阶段设计示意图如下：

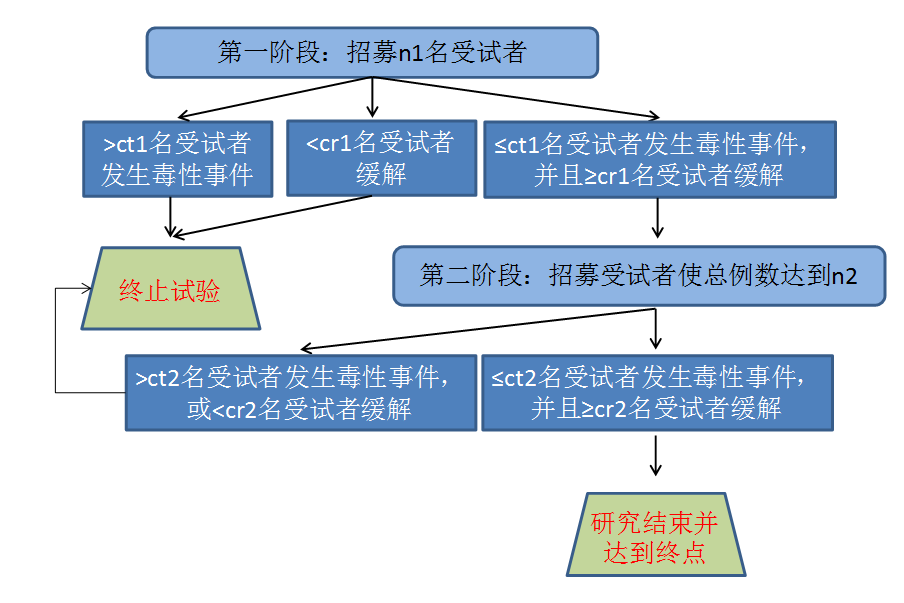
不同情况下同时考虑疗效和毒性的试验设计样本量计算如下表（调用SAS程序%Jin_Safety_Efficacy_Ph2）：

备注：上表中预设αr、αt和ß分别为0.15，0.05和0.20。theta表示疗效和毒性的相关性（theta=1表示不相关，theta大于1表示正相关）；PET0和ESS0分别指在原假设条件下（即疗效和毒性取值为Pr0，Pt0情况下）的最小提前终止概率和期望样本量。其它各参数对应含义如下:

cr1:第一阶段疗效临界值（缓解受试者小于此例数即不进入第二阶段）

ct1:第一阶段毒性临界值（缓解受试者大于此例数即不进入第二阶段）

cr2:第二阶段疗效临界值（缓解受试者小于此例数即认为未达到预设疗效不值得进一步开发）

ct2:第二阶段毒性临界值（缓解受试者大于此例数即认为毒性过大不值得进一步开发）

n1: 第一阶段所需受试者例数

n2: 两阶段所需总受试者例数

以上表第一行为例：对初始参数(Pr0/Pt0/Pr1/Pt1/theta)=(0.5/0.3/0.7/0.1/0.5)，初始显著性水平(αr/αt/ß)=(0.15/0.05/0.20)的试验设计，第一阶段入组15例受试者，如果其中缓解受试者例数小于9例或者发生毒性事件的受试者多于3例，则认为试验失败不进入第二阶段；如果缓解受试者例数大于等于9例或者发生毒性事件的受试者小于等于3例，则新增29例受试者，使总受试者例数达到44例。如果44例受试者中缓解例数小于25例或者发生毒性事件的例数多于8例，则认为试验失败，研究药物不值得进一步进行开发。

七、小结

综上，我们溯沿历史对肿瘤II期试验较常见的六种统计设计进行了粗浅的探讨，梳理成文，以飨读者。这些II期试验设计都局限在相同治疗的一组受试者中，没有同步对照和随机分组；都局限于1-2个招募阶段；主要采用基于肿瘤评估的客观缓解率进行设计和评价，可同时整合毒性效应，但没有纳入生存时间等疗效终点进行考虑。限于篇幅各种设计的复杂统计算法此文中均从略。

关于有随机分组的II期肿瘤试验，将择机在后续II期肿瘤试验的常用统计设计（二）中探讨。

八、参考文献

[1] Gehan EA. The determination of the number of patients required in a preliminary and a follow-up trial of a new chemotherapeutic agent. J Chronic Dis. 1961; 13(4): 346-353

[2] Agresti A., Coull BA. Approximate is better than “exact” for interval estimation of binomial proportions. The American Statistician 1998; 52: 119-126

[3] Fleming TR. One-sample multiple testing procedure for phase II clinical trials. Biometrics 1982;38:143-151

[4] Simon R. Optimal two-stage designs for phase II clinical trials. Control Clin Trials. 1989; 10 (1): 1-10.

[5] A P Mander, S G Thompson. Two-stage designs optimal under the alternative hypothesis for phase II cancer clinical trials. Contemp Clin Trials. 2010 Nov; 31(6): 572-8

[6] Yong Lin, Weichung J Shih. Adaptive two-stage designs for single-arm phase IIA cancer clinical trials. Biometrics. 2004 Jun; 60(2): 482-490

[7] Jung SH, Carey M, Kim KM. Graphical search for two-stage designs for phase II clinical trials. Controlled Clinical Trials 2001; 22: 367-372

[8] Sin-Ho Jung, Taiyeong Lee, KyungMann Kim, Stephen L George. Admissible two-stage designs for phase II cancer clinical trials. Stat Med. 2004 Feb 28; 23(4): 561-569

[9] Conaway MR, Petroni GR. Bivariate sequential designs for phase II trials. Biometrics 1995; 51: 656-64.

[10] Bryant J, Day R. Incorporating toxicity considerations into the design of two-stage phase II clinical trials. Biometrics 1995; 51: 1372-83.

[11] Jin H. Alternative designs of phase II trials considering response and toxicity. Contemporary Clinical Trials 2007, 28: 525-531.